Para descrever fluidos a altas temperaturas utilizamos a equação de estado PV=nRT que relaciona a pressão, o volume e a temperatura de uma dada quantidade n de moles do fluido. A baixas temperaturas (ou altas pressões) fluidos usuais sofrem uma mudança de fase termodinâmica, explicada somente quando levamos em consideração a interação intermolecular. O efeito médio destas interações resulta em correções ao gás ideal. A equação de Van der Waals (escrita aqui para um mol de fluido)

descreve qualitativamente bem tanto a fase líquida quanto a fase gasosa, assim como a transição entre as fases. Aqui v é o volume por mol, e a e b são constantes associadas a propriedades do fluido (ver aqui valores tabelados para distintos gases).

Abaixo de uma temperatura específica T_c as isotermas no diagrama PV apresentam uma região de coexistência, onde o fluido se separa em duas fases cujas energias livres de Gibbs por mol são necessariamente iguais g_gas=g_liq. Exatamente em T_c a região de coexistência se extingue (ou se reduz a um ponto). Determinamos T_c a partir de

Outra forma de encontrar o ponto crítico é reescrevendo a equação de terceiro grau para V na forma de um polinômio com raízes triplamente degeneradas e comparando com os termos da equação de Van der Waals

Encontramos que , e . Veja aqui uma tabela com valores de parâmetros críticos para diferentes fluidos.

Reescrevendo a equação de estado em termos das variáveis e obtemos a equação universal

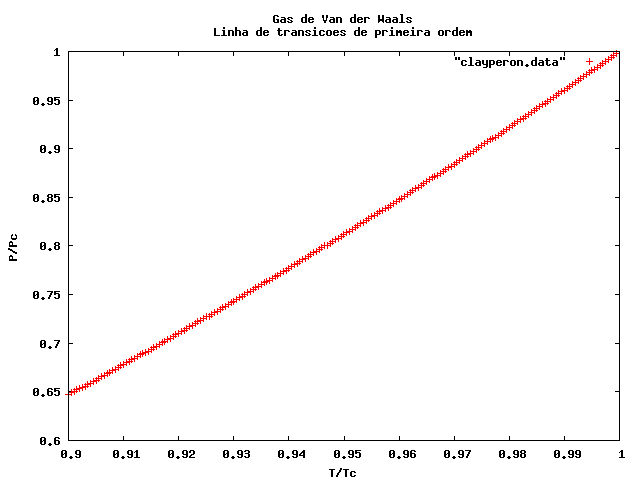
Para representar as diferentes isotermas no diagrama de Clayperon podemos resolver a equação cúbica em *V* para um dado *T* fixo. Buscando uma referência de cálculo numérico, como

vemos que dado o polinômio , calculamos as quantidades auxiliares

Se (R² < Q³) o polinômio possui 3 raízes reais distintas. Sendo

escrevemos as 3 raízes como

Caso (R² > Q³) só existe uma raiz real. Calculamos

e

onde sgn(x)=1 se x>0 e -1 se x<0 e abs(x) é o valor absoluto de x. A raiz é dada então por

onde (com T=0 se S=0).

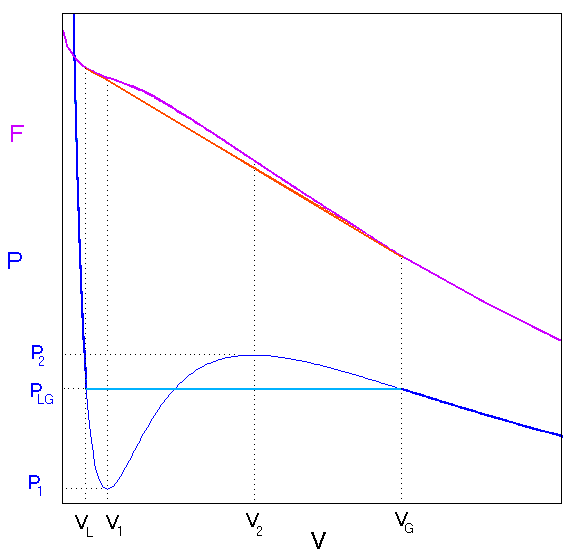
Vemos então que, para T<T_c, temos uma região do gráfico PV com 3 valores de v para cada valor de p. Parte desses valores (entre V₁ e V₂) se econtra em uma região onde a compressibilidade é negativa, representando o limite de estabilidade mecânica.

Para corrigir a teoria de Van der Waals adotamos a construção de Maxwell, que equivale a restaurar a concavidade da energia livre de Helmholtz F=U-TS. Os valores de v que definem a secante que “corrige” a energia livre de Helmholtz são identificados com os limites da região de coexistência, v_l e v_g.

Como as duas fases coexistentes se encontram em equilíbrio à mesma temperatura e pressão, g_liq=g_gas, com g=u-Ts+Pv ou g=f+Pv (as variáveis com letra minúscula estão normalizadas pelo número de moles),

Sendo temos que

e obtemos que

Note que isso equivale a dizer que as áreas definidas pela curva de Van der Waals e o retângulo definido por v_l e v_g devem ser iguais.

Assim, obtemos as curvas isotermas calculando, para cada valor de P entre limites desejados, o(s) valor(es) de V calculando as raízes pelo método acima. Para obter os valores de v_l e v_g associados com os limites da região de coexistência verificamos, quando T<T_c, se a igualdade acima é satisfeita. Caso isso aconteça, identificamos as duas raízes extremas com V_l e V_g.

Como não variamos continuamente a pressão, mas sim a incrementaremos de valores fixos e pequenos dP, assumimos uma tolerância na igualdade acima: para dP muito pequeno, a variação da área do quadrado do lado esquerdo da equação acima vale no máximo . Fixamos a tolerância em metade desse valor.

Quantidades de interesse que podemos obter com o procedimento acima:

• Isotermas no diagrama PV
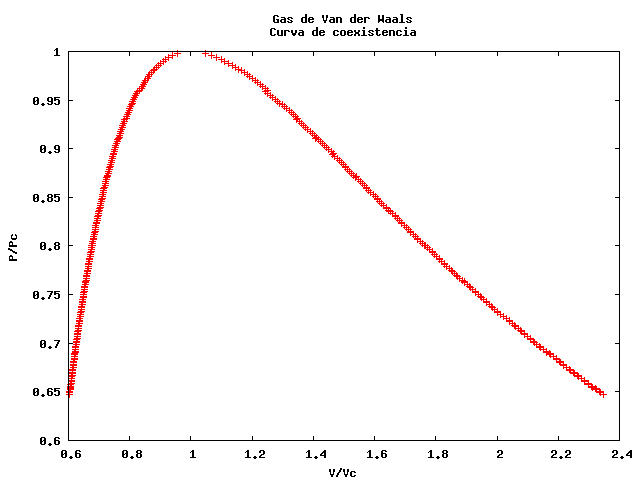
• Curva de coexistência
• Variação de entropia S_g-S_l para diferentes temperaturas.
• Calor latente como função da temperatura.

Curiosidades:

• Diagrama de fases do gelo e uma nova fase termodinâmica do gelo.

• Transformadas de Legendre em Física

• Definições para o potencial químico

Códigos em C e Perl para obtenção dos resultados acima: Download