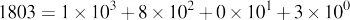Ferramentas de Computação em Física
Semana da Física 2011
Descreveremos neste tutorial como utilizar o computador como uma ferramenta no curso de Física. O sistema operacional utilizado será o Linux e faremos uso extensivo do terminal de linha de comando, que fornece uma maior compreensão dos processos envolvidos nas ações desejadas, como exibição dos arquivos em um diretório, alteração de nome de arquivos, criação e execução de programas criados pelo usuário, etc. Para aproveitar melhor esta apostila recomenda-se que o leitor possua conhecimento básico de informática: arquivos e estrutura de diretórios, execução de programas, etc.
O ambiente Linux
O sistema operacional Linux difere do Windows na maneira como o usuário interage com o sistema. No primeiro, diferente partes do sistema são organizadas em módulos (que possuem dependências particulares entre si) definindo uma estrutura descentralizada completamente configurável pelo usuário (o sistema operacional OS X da Apple possui várias similaridades com o Linux). A comunicação do usuário com o sistema se dá através de aplicativos cujos códigos-fonte podem ser livremente modificados pelo usuário.
O Linux foi originalmente desenvolvido por Linus Torvald em 1991 como alternativa para computadores pessoais do sistema operacional Unix, criado em 1969 por empregados do laboratório AT&T/Bell. Entre os criadores do Unix estão Dennis Ritchie e Brian Kernighan, que também criaram a linguagem de programação C e para ela traduziram em 1973 o Unix, que antes estava escrito em Assembler (O Linux foi originalmente desenvolvido em C). Veja abaixo uma breve história do sistemas operacionais Unix-like (como são chamados os sistemas que possuem a estrutura de núcleo central, ou kernel, e módulos).
Os computadores da sala de micro do alunos da graduação possui a distribuição Debian instalada. Uma grande vantagem do Linux, além do fato de ser um sistema de código aberto (leia sobre o projeto GNU), é sua extensa documentação: além de tutoriais na Internet ensinando como usar o sistema operacional, todos os comandos importantes possuem documentação que pode ser acessada através do comando man
Interação com o sistema operacional: linha de comando
Para entender melhor os processos envolvidos na execução de tarefas pelo sistema operacional
utilizaremos terminais de linha de comando. Ilustramos abaixo como abrir um terminal (chamado gnome-terminal neste caso) no Debian.

Uma vez que temos acesso a linhas de comando, podemos interagir com o sistema operacional e executar diversas tarefas. Ao abrirmos um terminal este, usualmente, aponta para o diretório principal (raiz) do usuário. Em geral o prompt padrão indica o diretório atual, o hostname da máquina e o nome do usuário (mas isto depende muito da distribuição Linux utilizada).
marcio@ssh1:~$
- Para saber o nome do usuário que abriu o terminal digite whoami
marcio@ssh1:~$ whoami marcio marcio@ssh1:~$
Uma grande vantagem do Linux é sua extensa documentação que inclui, além de tutoriais online, páginas de manual acessíveis pela linha de comando através do comando man <COMANDO>
marcio@pelego:~/cursos/escola2011$ man whoami
WHOAMI(1) User Commands WHOAMI(1)
NAME
whoami - print effective userid
SYNOPSIS
whoami [OPTION]...
DESCRIPTION
Print the user name associated with the current effective user ID. Same as id -un.
--help display this help and exit
--version
output version information and exit
AUTHOR
Written by Richard Mlynarik.
REPORTING BUGS
Report bugs to <bug-coreutils@gnu.org>.
COPYRIGHT
Copyright © 2008 Free Software Foundation, Inc. License GPLv3+: GNU GPL version 3 or
later <http://gnu.org/licenses/gpl.html>
This is free software: you are free to change and redistribute it. There is NO WAR
RANTY, to the extent permitted by law.
marcio@pelego:~/cursos/escola2011$
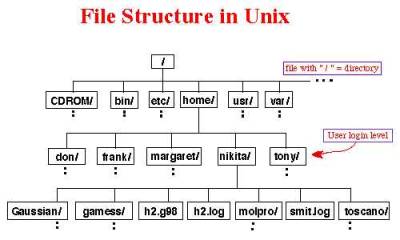
Estrutura de Arquivos
- Para saber em que diretório voce está digite pwd
marcio@ssh1:~$ pwd /home/docente/marcio marcio@ssh1:~$
- Para ver que arquivos se encontram no diretório que voce está digite ls
marcio@ssh1:~$ ls 2008.tgz lista1.tex agemodel1.c lista2.pdf agemodel2.c lista2.tex agemodel3.c lista4.tex agemodel4.c load-current.c agemodel.c lr-drp.c agemodel_final.c lyapunov from experiments.pdf marcio@ssh1:~$
- Para criar um diretório novo digite mkdir <NOVO DIR>
marcio@ssh1:~$ mkdir meudir
- Para entrar em um diretório específico que esteja um nível abaixo do que voce se encontra digite cd <DIR>
marcio@ssh1:~$ cd meudir marcio@ssh1:~/meudir$
- Para entrar em um diretório específico que esteja um nível acima do que voce se encontra digite cd ..
marcio@ssh1:~/meudir$ cd .. marcio@ssh1:~$
- Para remover um diretório específico que esteja um nível abaixo do que voce se encontra digite rm -f <DIR>
marcio@ssh1:~/meudir$ rm -f meudir marcio@ssh1:~$
Computadores em rede
Os computadores da sala dos alunos se encontram conectados em rede, e é possível se deslocar remotamente de uma máquina da rede para outra com comandos como telnet e ssh. A rede da sala dos alunos é centralizada em um servidor DHCP que fornece um endereço a cada computador nele conectadoIP (basicamente um nome composto de quatro números entre 0 e 255 separados por ponto) que gerencia a conexão de todos os micros da rede com a Internet.
Cada computador possui um endereço IP único dentro de sua sub-rede. Para saber o IP de sua máquina digite /sbin/ifconfig
No exemplo abaixo o computador está conectado ao servidor através da interface eth0 com o endereço IP 192.168.0.100
marcio@pelego:~/cursos/escola2011$ /sbin/ifconfig
eth0 Link encap:Ethernet HWaddr 00:24:21:c5:a2:b4
inet addr:192.168.0.100 Bcast:192.168.0.255 Mask:255.255.255.0
inet6 addr: fe80::224:21ff:fec5:a2b4/64 Scope:Link
UP BROADCAST RUNNING MULTICAST MTU:1500 Metric:1
RX packets:485944 errors:0 dropped:0 overruns:0 frame:0
TX packets:350354 errors:0 dropped:0 overruns:0 carrier:0
collisions:0 txqueuelen:1000
RX bytes:601797204 (573.9 MiB) TX bytes:41534569 (39.6 MiB)
Interrupt:221 Base address:0x4000
lo Link encap:Local Loopback
inet addr:127.0.0.1 Mask:255.0.0.0
inet6 addr: ::1/128 Scope:Host
UP LOOPBACK RUNNING MTU:16436 Metric:1
RX packets:80 errors:0 dropped:0 overruns:0 frame:0
TX packets:80 errors:0 dropped:0 overruns:0 carrier:0
collisions:0 txqueuelen:0
RX bytes:6904 (6.7 KiB) TX bytes:6904 (6.7 KiB)
marcio@pelego:~/cursos/escola2011$
- Para acessar remotamente outro computador utilize o comando ssh <USER>@<IP> onde <USER> é o nome do usuário na máquina a ser acessada e <IP> seu endereço de rede.
marcio@pelego:~/cursos/escola2011$ ssh marcio@200.20.9.67 marcio@200.20.9.67's password: Linux ssh1 2.6.26-2-686 #1 SMP Wed Aug 19 06:06:52 UTC 2011 i686 The programs included with the Debian GNU/Linux system are free software; the exact distribution terms for each program are described in the individual files in /usr/share/doc/*/copyright. Debian GNU/Linux comes with ABSOLUTELY NO WARRANTY, to the extent permitted by applicable law. Last login: Sun Oct 18 20:37:05 2011 from 189.24.43.87 marcio@ssh1:~$
Note que, além do endereço IP, cada máquina possui um nome (hostname) do tipo nome.domínio. Cada número IP é traduzido unicamente em um hostname. Podemos usar hostname ou IP quando nos referirmos a um computador.
marcio@pelego:~$ ssh marcio@ssh1.if.uff.br marcio@ssh1.if.uff.br's password: Linux ssh1 2.6.26-2-686 #1 SMP Wed Aug 19 06:06:52 UTC 2011 i686 The programs included with the Debian GNU/Linux system are free software; the exact distribution terms for each program are described in the individual files in /usr/share/doc/*/copyright. Debian GNU/Linux comes with ABSOLUTELY NO WARRANTY, to the extent permitted by applicable law. Last login: Sun Oct 18 23:29:33 2011 from 189.24.43.87 marcio@ssh1:~$
Editando arquivos
- Para apagar um arquivo utilize o comando rm <ARQ>
marcio@pelego:~/meudir$ ls extra newsclustering.pdf randoms.in total.out marcio@pelego:~/meudir$ rm total.out marcio@pelego:~/meudir$ ls extra newsclustering.pdf randoms.in marcio@pelego:~/meudir$
- Para mudar o nome de um arquivo utilize o comando mv <ARQ_OLD> <ARQ_NEW>
marcio@pelego:~/meudir$ ls extra newsclustering.pdf randoms.in marcio@pelego:~/meudir$ mv randoms.in random.in marcio@pelego:~/meudir$ ls extra newsclustering.pdf random.in marcio@pelego:~/meudir$
- Para copiar um arquivo utilize o comando cp <ORIGEM> <DESTINO>
marcio@pelego:~/meudir$ ls extra newsclustering.pdf random.in marcio@pelego:~/meudir$ cp random.in extra/othername.in marcio@pelego:~/meudir$ cd extra/ marcio@pelego:~/meudir/extra$ ls dull.c inside.conf othername.in marcio@pelego:~/meudir/extra$ cp dull.c ../dull.c marcio@pelego:~/meudir/extra$ cd .. marcio@pelego:~/meudir$ ls dull.c extra newsclustering.pdf random.in marcio@pelego:~/meudir$
* Para copiar um arquivo de uma máquina para outra utiliza o comando scp
marcio@pelego:~/meudir$ scp dull.c marcio@ssh1.if.uff.br:dullnew.c marcio@ssh1.if.uff.br's password: dull.c 100% 0 0.0KB/s 00:00 marcio@pelego:~/meudir$No exemplo acima o arquivo dull.c é copiado da máquina local (pelego) para a máquina remota (ssh1).
marcio@ssh1:~$ scp marcio@fiscomp.if.uff.int:mass_sp.c massnew.c marcio@fiscomp.if.uff.int's password: mass_sp.c 100% 2431 2.4KB/s 00:00 marcio@ssh1:~$No exemplo acima o arquivo mass_sp.c é copiado da máquina remota (fiscomp) para a máquina local (ssh1).
- Para criar ou editar um arquivo utilizamos um dos muitos editores de texto disponíveis em qualquer distribuição Linux. Exemplos incluem vi, nano, gedit,emacs entre outros. Vamos aqui utilizar o emacs, um editor de texto
bastante poderoso e amigável.
Suponha que voce obtenha em uma experiência de laboratório os dados:
| t(s) | v(cm/s) |
|---|---|
| 1 | 1.0 |
| 2 | 1.9 |
| 3 | 3.5 |
| 4 | 3.8 |
| 5 | 6.1 |
| 6 | 6.5 |
| 7 | 7.1 |
| 8 | 7.8 |
| 9 | 9.3 |
| 10 | 10.5 |
Vamos criar um arquivo com estes dados para posteriormente analisá-los. Na linha de comando digite emacs <ARQ> &. Repare o & no final do comando. Este símbolo tem como função executar o comando especificado e liberar o terminal para outros comandos.
marcio@pelego:~/meudir$ emacs exp1.data &
Caso voce nao inclua este comando o terminal ficará suspenso enquanto o comando for executado. Para recuperar o terminal, caso não utilize o comando & em sua chamada, aperte a tecla control (ctrl) e em seguida (sem soltar o ctrl) aperte z, ou ctrl-z resumidamente. Este comando libera o terminal e mantém o programa sendo executado em pausa. Para utilizar o programa digite bg após recuperar o terminal com ctrl-z
marcio@pelego:~/meudir$ emacs exp1.data ^Z [1]+ Stopped emacs exp1.data marcio@pelego:~/meudir$ bg [1]+ emacs exp1.data & marcio@pelego:~/meudir$
Digite seus dados no editor de texto e salve os resultados utilizando os comandos na barra superior do emacs ou digitando ctrl-x e em seguida, sem soltar o ctrl ctrl-s ou ctrl-x ctrl-s resumidamente.
Para verificar o conteúdo de arquivos-texto digite, na linha de comando, more <ARQ>
marcio@pelego:~/meudir$ more exp1.data 1 1.0 2 1.9 3 3.5 4 3.8 5 6.1 6 6.5 7 7.1 8 7.8 9 9.3 10 10.5 marcio@pelego:~/meudir$
Análise gráfica de dados
Para analisar graficamente a tabela de dados gerada na seção anterior podemos utilizar o gnuplot, um programa bastante leve e versátil, que pode gerar gráficos a partir de arquivos de dados com tabelas ou a partir de funções determinadas pelo usuário. Tambem podemos ajustar dados a funções arbitrariamente definidas (veja aqui um tutorial em português no formato pdf e esse excelente tutorial em inglês).
Para entrar no gnuplot digite, na linha de comando, gnuplot. Repare que neste caso não redirecionamos o comando para o background (com o &).
marcio@pelego:~/meudir$ gnuplot G N U P L O T Version 4.2 patchlevel 2 last modified 31 Aug 2007 System: Linux 2.6.26-2-686 Copyright (C) 1986 - 1993, 1998, 2004, 2007 Thomas Williams, Colin Kelley and many others Type `help` to access the on-line reference manual. The gnuplot FAQ is available from http://www.gnuplot.info/faq/ Send bug reports and suggestions to <http://sourceforge.net/projects/gnuplot> Terminal type set to 'wxt' gnuplot>
Experimente definir uma função arbitrária, como f(x)=sin(x)/x
gnuplot> f(x)=5.0*sin(x)/x gnuplot> plot f(x)
Vamos analisar os dados do experimento da seção anterior com o gnuplot. Para plotar o gráfico associado com os dados do arquivo exp1.data utilizamos o comando plot ”<ARQ>” (repare nas aspas em torno do nome do arquivo)
gnuplot> plot "exp1.data"
Podemos colocar linhas unindo os pontos com
gnuplot> set style data linespoints gnuplot> replot

Notamos que há uma tendência linear forte nos dados. Podemos utilizar o gnuplot para encontrar o melhor ajuste linear aos pontos experimentais (o gnuplot utiliza o método de Levenberg-Marquardt no ajuste). Definimos no gnuplot uma função linear f(x)=ax+b com dois parâmetros ajustáveis, a e b.
gnuplot> f(x)=a*x+b
e em seguida utilizamos o comando fit do gnuplot (para mais informações digite, dentro do gnuplot, help fit)
gnuplot> fit f(x) "exp1.data" via a,b
Iteration 0
WSSR : 1.47406 delta(WSSR)/WSSR : 0
delta(WSSR) : 0 limit for stopping : 1e-05
lambda : 4.4441
initial set of free parameter values
a = 1.02485
b = 0.113333
********************
After 1 iterations the fit converged.
final sum of squares of residuals : 1.47406
rel. change during last iteration : 0
degrees of freedom (FIT_NDF) : 8
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 0.429252
variance of residuals (reduced chisquare) = WSSR/ndf : 0.184258
Final set of parameters Asymptotic Standard Error
======================= ==========================
a = 1.02485 +/- 0.04726 (4.611%)
b = 0.113333 +/- 0.2932 (258.7%)
correlation matrix of the fit parameters:
a b
a 1.000
b -0.886 1.000
gnuplot>
Os melhores parâmetros encontrados, como mostra o resultado, foram a=1.02485 e b=0.113333. Podemos verificar a qualidade do resultado plotando as duas curvas no mesmo gráfico. Vamos também colocar labels nos eixos coordenados.
gnuplot> set xlabel "t(s)" gnuplot> set ylabel "v(cm/s)" gnuplot> plot "exp1.data" title "Dados experimentais",f(x) title "Melhor ajuste" gnuplot>
Vamos gerar uma figura com os resultados. O gnuplot pode salvar gráficos em diferentes formatos, como postscript, png, etc. Vamos salvar nosso resultado no formato png, que é vetorial e pode ser reescalado sem perda de resolução. Para isso redirecionamos a saída do programa para um arquivo png, fazemos um “replot” da figura, que será direcionada para o arquivo determinado, e redirecionamos a saída para x11 ou wxt.
gnuplot> set terminal png Terminal type set to 'png' Options are 'nocrop medium ' gnuplot> set output "exp1.png" gnuplot> replot gnuplot> set term wxt Terminal type set to 'wxt' Options are '0' gnuplot>
Enfim, salvamos o projeto que acabamos de gerar para podermos utiliza-lo sem necessidade de redigitar todos os comandos quando quisermos observar o gráfico no gnuplot novamente, e finalizamos o programa gnuplot
gnuplot> save "exp1.gnuplot" gnuplot> quit marcio@pelego:~/meudir$
Assim, podemos abrir o projeto novamente inicializando o gnuplot e utilizando o comando load ”<ARQ>” (repare nas aspas!)
Os dois arquivos que criamos devem estar no diretório de onde chamamos o gnuplot
marcio@pelego:~/meudir$ ls dull.c exp1.gnuplot extra newsclustering.pdf exp1.data exp1.png fit.log random.in marcio@pelego:~/meudir$
Linguagens de programação
Nos exemplos acima, quando digitamos comandos no terminal, estávamos realmente utilizando uma linguagem interpretada chamada de maneira geral de shell script (nas distribuições Linux atuais o mais utilizado é o bash). Para o processador central do computador executar instruções é preciso comunicá-las por meio de uma linguagem que o processador entenda. Essa linguagem é chamada de código de máquina, que é traduzida de maneira mnemônica pela linguagem Assembly. Tal linguagem, no entanto, requer enorme esforço de programação para a execução de tarefas simples. Com a popularização dos computadores surgiu a necessidade de formas mais simples de comunicação que tornassem o computador uma ferramenta acessível ao público leigo. Surge então algumas linguagens como C, Fortran, Perl e Python , sendo as duas primeiras exemplos de linguagem compilada e as últimas de linguagem interpretada (e todas as quatro são exemplos de linguage imperative. Em C e Fortran usamos um compilador, que traduz nosso programa para linguagem de máquina, enquanto Perl é interpretada no momento da execução por um programa (o interpretador).
Linguagens de computador, como línguas naturais (português, italiano, etc.), possuem um conjunto de operações básicas com as quais traduzimos algoritmos em ações. Vamos utilizar nesse tutorial a linguagem C para nos auxiliar com tarefas computacionais.
Números no computador
Antes de começarmos a programar temos que entender como o computador manipula números, os objetos principais de nossas análises.
Devido ao fato de termos dez dedos nas mãos, temos um sistema de contagem decimal, onde escrevemos um número qualquer como soma de múltiplos de potências de 10.
Os fatores multiplicativos das potências são números inteiros entre 0 e 9
Como a informação no computador é codificada em pulsos elétricos, e só existem dois estados possíveis (um pulso de corrente não nulo ou zero corrente), números têm que ser representados em uma base binária
Representamos esse último número de maneira abreviada como 11100001011. Cada componente do número é então representada por um bit,o “quantum” de informação, a menor medida definida pelo computador.
No computador temos números inteiros de 32 ou 64 bits, o que impõe um limite no maior número decimal que podemos representar.
Os números reais são representados de maneira menos direta (veja em http://www.psc.edu/general/software/packages/ieee/ieee.php mais detalhes). Para armazenar um número real, 6.5 por exemplo, os 32 bits (no caso de float) ou 64 bits (no caso de double) são reservados para o sinal, o expoente de uma potência de 2, e o termo fracionário do número (o número sempre é armazenado na forma 1.F * 2E).
S EEEEEEEE FFFFFFFFFFFFFFFFFFFFFFF 0 1 8 9 31
- Se E=255 e F é diferente de zero, então V=NaN (“Not a number”)
- Se E=255 e F=0 e S=1, então V=-infinito
- Se E=255 e F=0 e S=0, então V=infinito
- Se 0<E<255 então V=(-1)S * 2 (E-127) * (1.F)
- Se E=0 e F diferente de zero então V=(-1)S * 2 (-126) * (0.F)
- Se E=0 e F=0 e S=1, V=-0
- Se E=0 e F=0 e S=0, V=0
Exemplos:
0 00000000 00000000000000000000000 = 0
1 00000000 00000000000000000000000 = -0
0 11111111 00000000000000000000000 = Infinity
1 11111111 00000000000000000000000 = -Infinity
0 11111111 00000100000000000000000 = NaN
1 11111111 00100010001001010101010 = NaN
0 10000000 00000000000000000000000 = +1 * 2**(128-127) * 1.0 = 2
0 10000001 10100000000000000000000 = +1 * 2**(129-127) * 1.101 = 6.5
1 10000001 10100000000000000000000 = -1 * 2**(129-127) * 1.101 = -6.5
0 00000001 00000000000000000000000 = +1 * 2**(1-127) * 1.0 = 2**(-126)
0 00000000 10000000000000000000000 = +1 * 2**(-126) * 0.1 = 2**(-127)
0 00000000 00000000000000000000001 = +1 * 2**(-126) *
0.00000000000000000000001 =
2**(-149) (Menor valor positivo)
Linguagem C: primeiros passos
A linguagem C foi desenvolvida para a tradução de todo o sistema operacional UNIX, anteriormente escrito em Assembler. Devido ao grau de complexidade de um sistema operacional, entendemos porquê a linguagem C é tão poderosa e flexível. Tanto poder deve ser usado com cautela, pois riqueza de expressão sempre vêm acompanhada de mais possibilidades de erro!
Podemos representar números inteiros e reais em C com diferentes precisões:
| tipo | número de bits | alcance |
|---|---|---|
| char | 8 | -128 a 127 |
| signed int | 16 | -2147483648 a 2147483647 |
| unsigned int | 16 | 0 a 4294967295 |
| signed long int | 32 | -2147483648 a 2147483647 |
| unsigned long int | 32 | 0 a 4294967295 |
| float | 32 | 1.175494351×10–38 a 3.402823466×1038 (~6 digitos de precisão) |
| double | 64 | ~ -2.225074×10-308 a ~1.797693×10308 (~15 digitos de precisão) |
Esta definição vale para máquinas de 32 bits. Para descobrir os limites em sua máquina utilize as variáveis definidas em float.h e limits.h
Vamos aprender um pouco da linguagem C através de exemplos básicos e terminar com uma aplicação real, o ajuste linear de um conjunto de pontos pelo método dos mínimos quadrados. Existem vários tutoriais de programação na Internet, como s listados abaixo http://www.inf.pucrs.br/~pinho/LaproI/IntroC/IntroC.htm (Básico) http://www.inf.pucrs.br/~manssour/LinguagemC/ (Mais avançado) http://www.cs.cf.ac.uk/Dave/C/ (Em Inglês)
Passo a passo
O programa em C deve possuir uma função principal main e deve incluir um conjunto de bibliotecas (com funções e declarações de variáveis auxiliares)
// Texto à direita do símbolo // não é interpretado pelo compilador (comentário) // Esse programa imprime uma mensagem no terminal (stdio) #include<stdio.h> int main(void){ printf("Hello world\n"); return(0); }
Neste programa incluímos a biblioteca stdio. Depois criamos a função main, onde usamos o comando de impressão formatada printf. O texto entre aspas será impresso na tela. A sequência especial \n termina o texto com um line feed. Sem esse comando o prompt retornaria na mesma linha do texto. Experimente! Todas as linhas de execução em C terminam com ponto-e-vírgula (;) ! A função main retorna o valor 0, que pode ser usado em outros programas para indicar que o programa terminou sua execução normalmente.
O compilador
Para criar um código de máquina executável pelo processador usamos um compilador (no nosso caso o gcc). Salve o arquivo hello.c e digite
gcc hello.c -o hello -Wall
a flag -o serve para definirmos o nome do programa executável gerado, enquanto que a flag -Wall serve para que o compilador retorne não somente os erros, se existirem, mas também possíveis erros, como uso de variável para a qual não foi atribuído valor ou coisas do gênero. Digite man gcc para toda conhecer a funcionalidade do compilador.
Entrada e saída de dados (I/O)
As funções printf e scanf são as funções-padrão para entrada e saída de dados do terminal, e fprintf e fscanf seus análogos para entrada e saída de dados de arquivos.
// Esse programa imprime a soma de dois números reais no terminal (stdio) #include<stdio.h> int main(void){ double x,y,soma; printf("Entre com x: "); scanf("%lf",&x); printf("Entre com y: "); scanf("%lf",&y); soma=x+y; printf("x+y=%lf\n",soma); return(0); }
O comando scanf lê os dados digitados no terminal, e espera que ele seja de um dado tipo, neste caso, um real dupla precisão (double)
| entrada | tipo |
|---|---|
| %d | (signed) int |
| %u | unsigned int |
| %ld | signed long |
| %lu | unsigned long |
| %f | float |
| %e | float (notação científica) |
| %lf | double |
| %s | string of chars |
O primeiro scanf armazena o valor digitado no terminal na variável x (o “ampersand” & é uma tecnicalidade que indica somente que o scanf armazena no endereco de x o seu valor) e o segundo o valor de y.
A variável sum, também double (assim como em qualquer operação aritmética, devemos operar sempre com o mesmo tipo de variáveis!), assume o valor da soma de x e y.
O último printf retorna o texto entre aspas para o terminal, substituindo %lf pelo valor da variável sum.
// Esse programa lê um arquivo com 2 colunas (x,y) de números reais e grava outro arquivo // com 3 colunas contendo (i,x+y,x*y,log(x)+log(y)) onde i é um contador de linhas // A função logaritmo está definida na biblioteca math.h #include<stdio.h> #include<math.h> int main(void){ double x,y,soma,produto,logaritmo; int i; char in_file[100]; // O nome do arquivo deve conter no máximo 100 caracteres FILE *in_ptr,*out_ptr; printf("Nome do arquivo: "); scanf("%s",in_file); // Lê o nome do arquivo in_file in_ptr=fopen(in_file,"r"); // abre o arquivo in_file para leitura out_ptr=fopen("log.data","w"); // abre o arquivo log.data para escrita i=0; // inicializa a variavel i com o valor 0 fscanf(in_ptr,"%lf %lf",&x,&y); while(!feof(in_ptr)){ // enquanto não chegar o fim do arquivo soma=x+y; produto=x*y; logaritmo=log(x)+log(y); fprintf(out_ptr,"%d %lf %lf %lf\n",i,soma,produto,logaritmo); // imprime no arquivo i++; // incrementa o valor de i fscanf(in_ptr,"%lf %lf",&x,&y); }; printf("Foram lidas %d linhas\n",i); fclose(in_ptr); // fecha arquivo in_ptr fclose(out_ptr); // fecha arquivo out_ptr return(0); }
Compilamos esse programa incluindo a chamada para a biblioteca matemática math.h (É boa prática criar executáveis com o mesmo nome do programa-fonte .c)
marcio@ssh1:~$ gcc log.c -o log -lm -Wall
E executamos colocando os caracteres ./ na frente do executável (Pois o diretório atual não necessariamente estará incluído no PATH de sua distribuição Linux).
marcio@ssh1:~$ ./log nome do arquivo: exp1.data marcio@ssh1:~$
Podemos confirmar o resultado de nossas operações utilizando a capacidade do gnuplot de manipular o valor das colunas de dados e plotá-las como eixos ordenados.
marcio@pelego:~/cursos/escola2011$ gnuplot
G N U P L O T
Version 4.2 patchlevel 2
last modified 31 Aug 2007
System: Linux 2.6.26-2-686
Copyright (C) 1986 - 1993, 1998, 2004, 2007
Thomas Williams, Colin Kelley and many others
Type `help` to access the on-line reference manual.
The gnuplot FAQ is available from http://www.gnuplot.info/faq/
Send bug reports and suggestions to <http://sourceforge.net/projects/gnuplot>
Terminal type set to 'wxt'
gnuplot> pl "log.data" us 2:3,"exp1.data" us ($1+$2):($1*$2)
gnuplot>
Vamos terminar com uma aplicação real, o ajuste linear de um conjunto de pontos pelo método dos mínimos quadrados. Dado um conjunto de N pares (x,y), como o do arquivo exp1.data que visualisamos com o gnuplot, podemos fazer um ajuste linear y=ax+b aos pontos onde (ver aqui mais detalhes sobre o método]]
Vamos entrar com o arquivo de dados como parâmetro de entrada do programa através dos parâmetros argc e argv da funão main.
#include<stdio.h> #include<math.h> #define MAXPOINTS 1000 int main(int argc, char *argv[]){ int i,N; double x[MAXPOINTS],y[MAXPOINTS],sum_x,sum_x2,sum_y,sum_y2, sum_xy,a,b,yf,sxx,syy,sxy,s,error_a,error_b; char arq[100]; FILE *in_ptr,*out_ptr; printf("Ajuste linear y=ax+b pelo metodo dos minimos quadrados\n"); printf("Lendo arquivo %s\n",argv[1]); in_ptr=fopen(argv[1],"r"); N=0; fscanf(in_ptr,"%lf %lf",&x[N],&y[N]); while(!feof(in_ptr)){ N++; fscanf(in_ptr,"%lf %lf",&x[N],&y[N]); } printf("Arquivo contem %d pontos\n",N); sum_x=0.0; sum_x2=0.0; sum_y=0.0; sum_y2=0.0; sum_xy=0.0; for(i=0;i<N;i++){ sum_x=sum_x + x[i]; sum_x2=sum_x2 + (x[i]*x[i]); sum_y=sum_y + y[i]; sum_y2=sum_y2 + (y[i]*y[i]); sum_xy=sum_xy + (x[i]*y[i]); } sxx = sum_x2*(double)N-sum_x*sum_x; syy = sum_y2*(double)N-sum_y*sum_y; sxy = sum_xy*(double)N-sum_x*sum_y; a = sxy/sxx; b = (sum_y*sum_x2 - sum_x*sum_xy)/(sum_x2*(double)N - sum_x*sum_x); s = sqrt((syy-b*sxy)/(double)(N-2)); // Calculo do desvio padrao (estimativa de erro) dos parametros error_a=s*sqrt((1.0/(double)N) + (sum_x*sum_x/sum_x2)); error_b=s/sqrt(sxx); printf("Valores encontrados: a=%lf(%lf) b=%lf(%lf)\n",a,b,error_a,error_b); sprintf(arq,"fit-N%d.data",N); out_ptr=fopen(arq,"w"); for(i=0;i<N;i++){ yf=a*x[i]+b; fprintf(out_ptr,"%lf %lf %lf\n",x[i],y[i],yf); } fclose(out_ptr); printf("Parametros encontrados: a=%lf, b=%lf\n",a,b); return(0); }
Compile o programa least.c incluindo a biblioteca math.h
marcio@pelego:~/cursos/escola2011$ gcc least.c -o least -lm -Wall marcio@pelego:~/cursos/escola2011$
Rode o programa fornecendo o arquivo exp1.data como parâmetro de entrada
marcio@pelego:~/cursos/escola2011$ ./least exp1.data 1.175494e-38 3.402823e+38 2.225074e-308 1.797693e+308 Ajuste linear y=ax+b pelo metodo dos minimos quadrados Lendo arquivo exp1.data Arquivo contem 10 pontos Valores encontrados: a=1.024848(0.113333) b=27.950296(0.344970) Parametros encontrados: a=1.024848, b=0.113333 marcio@pelego:~/cursos/escola2011$
Vamos usar novamente o gnuplot para conferir nosso resultado
marcio@pelego:~/cursos/escola2011$ gnuplot G N U P L O T Version 4.2 patchlevel 2 last modified 31 Aug 2007 System: Linux 2.6.26-2-686 Copyright (C) 1986 - 1993, 1998, 2004, 2007 Thomas Williams, Colin Kelley and many others Type `help` to access the on-line reference manual. The gnuplot FAQ is available from http://www.gnuplot.info/faq/ Send bug reports and suggestions to <http://sourceforge.net/projects/gnuplot> Terminal type set to 'wxt' gnuplot> plot "fit-N10.data" with linespoints title "Data","" using 1:3 with lp with linespoints title "Best fit" gnuplot> set key left gnuplot> replot gnuplot> set xlabel "t(s)" gnuplot> set ylabel "v(cm/s)" gnuplot> replot gnuplot> set title "Ajuste pelo metodo dos minimos quadrados" gnuplot> replot
gnuplot> f(x)=a*x+b
gnuplot> fit f(x) "fit-N10.data" using 1:2 via a,b
Iteration 0
WSSR : 7.15 delta(WSSR)/WSSR : 0
delta(WSSR) : 0 limit for stopping : 1e-05
lambda : 4.4441
initial set of free parameter values
a = 1
b = 1
/
Iteration 1
WSSR : 2.81548 delta(WSSR)/WSSR : -1.53953
delta(WSSR) : -4.33452 limit for stopping : 1e-05
lambda : 0.44441
resultant parameter values
a = 0.916407
b = 0.902441
/
Iteration 2
WSSR : 1.48391 delta(WSSR)/WSSR : -0.897341
delta(WSSR) : -1.33157 limit for stopping : 1e-05
lambda : 0.044441
resultant parameter values
a = 1.01511
b = 0.181115
/
Iteration 3
WSSR : 1.47406 delta(WSSR)/WSSR : -0.00667955
delta(WSSR) : -0.00984607 limit for stopping : 1e-05
lambda : 0.0044441
resultant parameter values
a = 1.02484
b = 0.113397
/
Iteration 4
WSSR : 1.47406 delta(WSSR)/WSSR : -5.89824e-09
delta(WSSR) : -8.69436e-09 limit for stopping : 1e-05
lambda : 0.00044441
resultant parameter values
a = 1.02485
b = 0.113333
After 4 iterations the fit converged.
final sum of squares of residuals : 1.47406
rel. change during last iteration : -5.89824e-09
degrees of freedom (FIT_NDF) : 8
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 0.429252
variance of residuals (reduced chisquare) = WSSR/ndf : 0.184258
Final set of parameters Asymptotic Standard Error
======================= ==========================
a = 1.02485 +/- 0.04726 (4.611%)
b = 0.113333 +/- 0.2932 (258.7%)
correlation matrix of the fit parameters:
a b
a 1.000
b -0.886 1.000
gnuplot>
Como era de se esperar, obtemos o mesmo resultado que no gnuplot! Confira os valores de a e b encontrados.
Discretização de derivadas: o pêndulo simples
Muitas leis Físicas são formuladas através de equações diferenciais: as equações de Maxwell do Eletromagnetismo, a segunda lei de Newton, a equação de Schrödinger, etc.
No entanto, operações no computador acontecem em tempos discretos, com a transmissao de pulsos elétricos a uma frequência da ordem de bilhões de pulsos por segundo nos computadores de hoje em dia. Como vimos antes, números reais também são armazenados com precisão finita, de modo que devemos inevitavelmente trabalhar com aproximações discretas para derivadas se quisermos utilizar o computador como uma ferramenta capaz de simular processos físicos.
Vamos utilizar o método de Euler para discretizar a derivada de uma função (acesse o site de aulas do MIT para maiores detalhes sobre este e outros métodos mais precisos de discretização). Para exemplificar o método vamos resolver o problema de um pêndulo balístico que recebe o impacto de um corpo e adquire uma velocidade v0
Decompomos a força gravitacional que atua no conjunto de massas após a colisão em componentes radial (ao longo da haste que segura os corpos) e tangencial e escrevemos
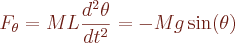
onde escrevemos

Eliminando a massa do problema obtemos a equação diferencial de segunda ordem

Tal equação não possui solução analítica fechada, mas para pequenas velocidades, que correspondem a pequena amplitude angular dada por

podemos fazer a aproximação  e encontrar a solução do problema para pequenas oscilações
e encontrar a solução do problema para pequenas oscilações
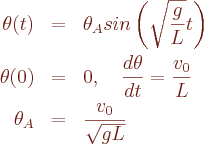
O método de Euler
Apesar de não possuir solução analítica, podemos determinar a evolução do pêndulo de maneira aproximada através da discretização da derivada  . O método de Euler consiste essencialmente em substituir a tangente no ponto t de uma curva
. O método de Euler consiste essencialmente em substituir a tangente no ponto t de uma curva  (derivada no ponto) pela secante
(derivada no ponto) pela secante
e identificamos h com a discretização da derivada,  .
.

A precisão do método é dada pelo tamanho do passo h de discretização (acesse o site de aulas do MIT para maiores detalhes sobre este e outros métodos mais precisos de discretização).
Assim, calculamos

e

A derivada segunda nada mais é do que a derivada da derivada

que obtemos usando as expressões encontradas para a derivada primeira,
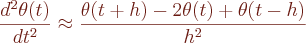
Obtemos finalmente a equação de diferenças

Assim, sendo h o tamanho do passo de iteração, escrevemos os valores  como
como 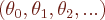 e
reescrevemos a equação acima como
e
reescrevemos a equação acima como

com

O código abaixo implementa este método, com o qual podemos fazer um estudo da dependência do período do pêndulo com a amplitude de oscilação.
#include<stdio.h> #include<math.h> #define PI 3.14159265 int main(void){ double theta,theta_ant,theta_ant2,theta_teo,theta_max,v_teo, ampl,v,g,L,t,dt,dt2,tf,gl,w,vmax; unsigned long n,nmax; char fname[100]; FILE *fout; printf("###### Calculo da trajetoria do pendulo simples #####\n"); printf("Comprimento do fio (cm): "); scanf("%lf",&L); printf("Aceleracao da gravidade (cm/s^2): "); scanf("%lf",&g); // Com essa velocidade o pêndulo alcança a posição horizontal vmax=sqrt(2.0*g*L); do{ printf("Velocidade incial deve ser menor que %lf\n",vmax); printf("Velocidade inicial (cm/seg): "); scanf("%lf",&v); if(v>vmax){ printf("Com esta velocidade o angulo maximo eh maior que 45 graus!\n"); } }while(v>vmax); theta_max=acos((L-v*v/(2.0*g))/L)*180.0/3.14; printf("Angulo maximo atingido=%lf graus\n",theta_max); printf("Tempo de simulacao (segundos): "); scanf("%lf",&tf); printf("Discretizacao (dt) do tempo: "); scanf("%lf",&dt); // Pendulo inicialmente parado recebe impulso // que o faz adquirir velocidade inicial v theta_ant2=0.0; theta_ant=(v/L)*dt; // Evolucao de um passo (met. de Euler) gl=g/L; dt2=dt*dt; ampl=v/sqrt(g*L); w=sqrt(g/L); // Grava arquivo e inclui no nome // Comprimento do fio L (com 2 casas decimais) // Velocidade inicial vi (com 1 casa decimal) // Acel. da gravidade g (com 1 casa decimal) // Discretizacao dt (com 4 casas decimais) sprintf(fname,"theta-L%.2lf-vi%.1lf-g%.1lf-dt%.4lf.out",L,v,g,dt); fout=fopen(fname,"w"); // dt=(tf-t0)/nmax // tf=t0+nmax*dt com t0=0 nmax=(unsigned long)(tf/dt); // numero de passos até atingir tf for(n=0;n<nmax;n++){ theta=2.0*theta_ant-gl*dt2*sin(theta_ant)-theta_ant2; // Velocidade linear em cm/s no instante theta_ant v=L*(theta-theta_ant2)/dt; theta_ant2=theta_ant; theta_ant=theta; t=((double)n)*dt; // tempo em segundos theta_teo=(180.0/PI)*ampl*sin(w*t); // Solucao para pequenos angulos v_teo=L*ampl*w*cos(w*t); // Solucao para pequenos angulos // imprimindo angulo em graus e velocidade em cm/s fprintf(fout,"%lf %lf %lf %lf %lf %lf\n", t,theta*(180.0/PI),theta_ant*(180.0/PI),v,theta_teo,v_teo); } fclose(fout); printf("Dados salvos em %s\n",fname); return(0); }
Compilamos este programa com chamada para a biblioteca matemática -lm. Como estamos aumentando a complexidade do problema, que envolve mais operações a serem feitas pelo processador, é bom pensarmos em otimização do código. No compilador gcc existem algumas flags que habilitam algumas otimizações feitas pelo compilador (como replicar o código N vezes e remover o loop for que seria realizado N vezes, evitando assim o teste condicional da variável envolvida em cada iteração do loop for). Vamos utilizar a flag -O3 (man gcc para saber mais).
marcio@pelego:~/cursos/semana2011$ gcc -O6 -o pendulum pendulum.c -lm -Wall marcio@pelego:~/cursos/semana2011$ marcio@pelego:~/cursos/semana2011$ ./pendulum ###### Calculo da trajetoria do pendulo simples ##### Comprimento do fio (cm): 20.0 Aceleracao da gravidade (cm/s^2): 980.0 Velocidade incial deve ser menor que 197.989899 Velocidade inicial (cm/seg): 20.0 Angulo maximo atingido=8.196243 graus Tempo de simulacao (segundos): 10.0 Discretizacao (dt) do tempo: 0.001 Dados salvos em theta-L20.00-vi20.0-g980.0-dt0.0010.out marcio@pelego:~/cursos/semana2011$
Usaremos o gnuplot para analisar os resultados. Utilizaremos mais uma funcionalidade do gnuplot: a capacidade de utilização de fontes gregas (com o comando {/Symbol <TEXTO>}) e subscrito (com underscore _). Gravaremos a imagem no formato postscript, que é o mais apropriado para se exportar para artigos científicos escritos no formato latex (é essencial colocar a saída no formato enhanced!).
marcio@pelego:~/cursos/semana2011$ gnuplot
G N U P L O T
Version 4.2 patchlevel 2
last modified 31 Aug 2007
System: Linux 2.6.26-2-686
Copyright (C) 1986 - 1993, 1998, 2004, 2007
Thomas Williams, Colin Kelley and many others
Type `help` to access the on-line reference manual.
The gnuplot FAQ is available from http://www.gnuplot.info/faq/
Send bug reports and suggestions to <http://sourceforge.net/projects/gnuplot>
Terminal type set to 'wxt'
gnuplot> set yrange[-5:10]
gnuplot> se title " Pendulo balistico \n Velocidade inicial v_0=10 cm/s --> {/Symbol q}_{max}=4.10"
gnuplot> set xlabel "t(s)"
gnuplot> se yl "{/Symbol q}(graus)"
gnuplot> plot "theta-L20.00-vi10.0-g980.0-dt0.0010.out" using 1:2 with linespoints title "Solucao numerica","" us 1:5 with linespoints plot "theta-L20.00-vi10.0-g980.0-dt0.0010.out" using 1:2 with linespoints title "Solucao numerica","" us 1:5 with linespoints title "Ap us 1:5 with lines title "Aprox. de pequenos angulos",acos((20-10*10/(2.0*980))/20.0)*180.0/3.14 title "Angulo maximo"
gnuplot> save "theta-L20.00-vi10.0-g980.0-dt0.0010.gnp"
gnuplot> set terminal postscript enhanced color
Terminal type set to 'postscript'
Options are 'landscape enhanced defaultplex \
leveldefault color colortext \
dashed dashlength 1.0 linewidth 1.0 butt \
palfuncparam 2000,0.003 \
"Helvetica" 14 '
gnuplot> set output "theta-L20.00-vi10.0-g980.0-dt0.0010.ps"
gnuplot> replot
gnuplot> set terminal wxt
Terminal type set to 'wxt'
Options are '0'
gnuplot> quit
Plotamos também nesse gráfico a amplitude de oscilação 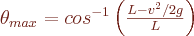
Podemos ver nossa figura com o programa evince
marcio@pelego:~/cursos/semana2011$ evince compare_pendulum.ps marcio@pelego:~/cursos/semana2011$
Vemos que a solução numérica coincide perfeitamente com a aproximação analítica para pequenos ângulos para baixas velocidades iniciais.
Aumentando a velocidade inicial de 10 cm/s para 50 cm/s percebemos um ligeiro aumento do período de oscilação.
Aumentando ainda mais a velocidade inicial a discrepância cresce visivelmente, indicando um aumento significativo do período.
O que acontece com o movimento do pêndulo na Lua? Para uma mesma velocidade de impacto com uma massa menor, o sistema se move inicialmente com a mesma velocidade, tanto na Terra quanto na Lua (pois isso só depende da validade da hipótese de conservação da energia). Qual o movimento resultante? A amplitude angular muda? E o período de oscilação? Pela solução do problema vemos que ambos devem mudar.
**Desafio**: Implemente uma força de atrito dependente da velocidade. Voce consegue analisar o decaimento exponencial da amplitude angular com o tempo?**
Publicação do resultado
Para publicar nosso resultado em um formato livre, independente de máquina e com qualidade de revista, utilizamos o Latex. Um exemplo de como escrever um código latex segue abaixo (voce pode utilizar qualquer editor para escrever o código)
\documentclass[12pt]{article} \usepackage{graphicx}% Include figure files \begin{document} %% Exemplo de um arquivo latex %% Os comandos parecem razoavelmente auto-explicativos %%%%%%%%%%%% \title{An\'alise num\'erica do p\^endulo simples} \author{Marcio Argollo de Menezes\\Instituto de F\'{\i}sica, Universidade Federal Fluminense, Niter\'oi, RJ, Brasil.} \maketitle \begin{abstract} \noindent Utilizaremos o m\'etodo de Euler para discretizar a equa\c{c}\~ao de movimento do p\^endulo simples em um campo gravitacional constante. \end{abstract} % Repare nas sequencias especiais para colocar acentuacao nas palavras \section{Introdu\c{c}\~ao} Vamos resolver numericamente o problema de um p\^endulo bal\'{\i}stico que recebe o impacto de um corpo e adquire uma velocidade $v_0$. Este problema possui solu\c{c}\~ao aproximada apenas no caso de pequenas oscila\c{c}\~oes. Para resolver numericamente o problema usamos o m\'etodo de Euler e escrevemos \begin{eqnarray*} \frac{d^2 \theta(t)}{dt^2}+ \frac{g}{L} \times \sin(\theta(t))=0 \\ \theta(0)=0~~e~~\frac{d \theta}{dt}_{t=0}=\frac{v_0}{L} \end{eqnarray*} como \begin{eqnarray*} \theta_{n+1}\approx 2\theta_{n} - \frac{g}{L}sin\left(\theta_n\right)h^2 -\theta_{n-1} \end{eqnarray*} Onde $h$ \'e o tamanho da discretiza\c{c}\~ao do intervalo, que fazemos ir a zero na defini\c{c}\~ao de derivada. \begin{figure}[!htbp] \begin{center} \includegraphics[width=0.8\columnwidth,angle=0]{theta-l20.00-vi10.0-g980.0-dt0.0010.ps} \end{center} \caption{O problema do p\^endulo bal\'{\i}stico, solu\c{c}\~ao num\'erica.} \label{fig_sol} \end{figure} \begin{thebibliography}{40} \bibitem{mit} Acesse o site de aulas do MIT (http://web.mit.edu/10.001/Web/ Course\_notes/Differential\_Equations\_Notes/lec24.html) para maiores detalhes sobre este e outros métodos mais precisos de discretização \end{thebibliography} \end{document}
Para transformar esse código em uma imagem de texto com figuras utilizamos o comando latex no terminal
marcio@tsallis:~/cursos/semana2011$ latex template.tex This is pdfTeX, Version 3.1415926-1.40.10 (TeX Live 2011/Arch Linux) restricted \write18 enabled. entering extended mode (./template.tex LaTeX2e <2005/12/01> Babel <v3.8l> and hyphenation patterns for english, usenglishmax, dumylang, noh yphenation, german-x-2011-06-19, ngerman-x-2011-06-19, ancientgreek, ibycus, ar abic, basque, bulgarian, catalan, pinyin, coptic, croatian, czech, danish, dutc h, esperanto, estonian, farsi, finnish, french, galician, german, ngerman, mono greek, greek, hungarian, icelandic, indonesian, interlingua, irish, italian, ku rmanji, latin, latvian, lithuanian, mongolian, mongolian2a, bokmal, nynorsk, po lish, portuguese, romanian, russian, sanskrit, serbian, slovak, slovenian, span ish, swedish, turkish, ukenglish, ukrainian, uppersorbian, welsh, loaded. (/usr/share/texmf-dist/tex/latex/base/article.cls Document Class: article 2005/09/16 v1.4f Standard LaTeX document class (/usr/share/texmf-dist/tex/latex/base/size12.clo)) (/usr/share/texmf-dist/tex/latex/graphics/graphicx.sty (/usr/share/texmf-dist/tex/latex/graphics/keyval.sty) (/usr/share/texmf-dist/tex/latex/graphics/graphics.sty (/usr/share/texmf-dist/tex/latex/graphics/trig.sty) (/usr/share/texmf/tex/latex/config/graphics.cfg) (/usr/share/texmf-dist/tex/latex/graphics/dvips.def))) (./template.aux) Overfull \hbox (73.9477pt too wide) in paragraph at lines 11--11 [][] <theta-l20.00-vi10.0-g980.0-dt0.0010.ps> Underfull \hbox (badness 1087) in paragraph at lines 54--59 []\OT1/cmr/m/n/12 Acesse o site de aulas do MIT (http://web.mit.edu/10.001/Web/ Underfull \hbox (badness 4940) in paragraph at lines 54--59 \OT1/cmr/m/n/12 Course[]notes/Differential[]Equations[]Notes/lec24.html) para m aiores [1] [2] (./template.aux) ) (see the transcript file for additional information) Output written on template.dvi (2 pages, 3064 bytes). Transcript written on template.log. marcio@tsallis:~/cursos/semana2011$
Eventualmente o latex pode pedir para voce executar o comando de novo.
LaTeX Warning: Label(s) may have changed. Rerun to get cross-references right.
Isso acontece, por exemplo, quando há referências a figuras ou tabelas no texto (Para saber mais leia esse ou esse tutorial. Para saber mais sobre como escrever equações no Latex acesse esse site).
Após esse comando o Latex irá gerar (entre outros) um arquivo no formato DVI. Podemos utilizar o comando xdvi para visualizar esse arquivo
marcio@tsallis:~/cursos/semana2011$ xdvi template.dvi & [2] 28175 marcio@tsallis:~/cursos/semana2011$
Mas o melhor é gerar um arquivo PDF
marcio@tsallis:~/cursos/semana2011$ dvipdf template.dvi marcio@tsallis:~/cursos/semana2011$
e ver a figura com o evince ou acroread
marcio@tsallis:~/cursos/semana2011$ evince template.pdf & [3] 28205 marcio@tsallis:~/cursos/semana2011$