Nuno Crokidakis

paris_palestra.jpg ASCII���User comments

Fotos: Seminário numa conferência de Socio-Física, na Ecole Polytechnique (Paris, 2011) - Vista do Campus da UFF para a Baía de Guanabara, com o Pão de Açúcar e o Corcovado ao fundo

“A verdadeira lógica deste mundo está no cálculo de probabilidades.” - James Clerk Maxwell

Change Language: English

Atenção Alunos: Informações sobre as Disciplinas podem ser encontradas no fim da página.

Bem vindo à minha página! Sou doutor em física e professor adjunto do Instituto de Física da Universidade Federal Fluminense. Minha área de atuação é a modelagem estatística e computacional de Sistemas Complexos. Em outras palavras, o meu interesse é o estudo de sistemas constituídos por um grande número de unidades que interagem entre si. Como exemplos temos neurônios no cérebro, spins em um sistema magnético, corretores no mercado financeiro, proteínas em uma rede metabólica, pessoas com diferentes opiniões em um grupo ou população, carros em estradas, indivíduos doentes e saudáveis em uma dada população e muitos outros. Trata-se de uma área interdisciplinar cujo objetivo é o entendimento do comportamento macroscópico de um dado sistema a partir do estudo das propriedades estatísticas do seus constituintes microscópicos. Em analogia com a Física Estatística usual, aparecem rotineiramente nestes sistemas correlações de longo alcance, leis de potência e transições de fase do tipo ordem-desordem, daí o interesse de físicos por sistemas complexos.

A linha de trabalho que mais tenho atacado nos últimos anos é a Modelagem de Fenômenos Sociais. A relação destes sistemas com a Física mais tradicional não é somente pela ocorrência de Fenômenos Críticos em ambos. Assim como os modelos da Física Estatística explicam por exemplo como uma coleção de átomos pode exibir o comportamento correlacionado necessário para produzir um ferromagneto, os modelos que representam Fenômenos Sociais pretendem explicar comportamentos interdependentes. A idéia básica da Física Estatística - que o comportamento de um átomo é influenciado pelo comportamento dos outros átomos - é, portanto, semelhante à afirmação das Ciências Sociais de que as decisões de um indivíduo dependem das decisões dos outros; aí que reside a possibilidade de uma estrutura matemática e/ou computacional comum. Uma discussão interessante sobre esta relação pode ser encontrada no artigo de Steven Durlauf, How can statistical mechanics contribute to social science?

Meu CV na plataforma Lattes pode ser encontrado aqui.

As minhas áreas de interesse estão descritas em mais detalhes abaixo, e alguns dos estudos que fiz resultaram nas publicações a seguir. Os preprints podem ser acessados facilmente no Arxiv, e as citações no Google Scholar. Alguns destaques são dados logo abaixo.

Destaques em Pesquisa

Um trabalho nessa linha saiu recentemente em colaboração com Allan Vieira e Celia Anteneodo. Propusemos um modelo onde as opiniões dos agentes são representadas por números reais no intervalo [-1,1], onde o sinal representa uma posição (contra ou a favor, por exemplo), e o valor representa quão extremista (próximo de +1 ou -1) ou moderado (mais próximo de 0) um indivíduo é em relação ao tema em debate. Introduzindo comportamentos contrários, independentes e considerando também a convicção dos indivíduos, vimos que a emergência de extremismo em uma população pode ser associada com a existência de indivíduos com fortes convicções positivas com respeito às suas opiniões, além de baixa fração de escolhas independentes. Por outro lado, a ocorrência de comportamentos independentes, assim como a existência de agentes que mudam de posição (de contra pra a favor e vice versa) espontaneamente leva à dominância de indivíduos com posições moderadas. O artigo foi publicado no Journal of Statistical Mechanics, e pode ser encontrado neste link.

Um outro trabalho nessa linha de dinâmicas sociais saiu recentemente em colaboração com Paulo Murilo Castro de Oliveira. Propusemos um modelo que simula o comportamento de indivíduos em discussões de um tema com 2 opções (sim/não em uma pesquisa, por exemplo). O modelo mostrou que opiniões majoritárias podem ser revertidas e se tornarem minoritárias, e que por trás disso está um mecanismo semelhante a um fenômeno biológico chamado de Gargalo de Darwin. O artigo foi publicado na Physica A, e pode ser encontrado neste link.

Recentemente fizemos um estudo sobre Eleições Brasileiras, em colaboração com Celia Anteneodo e Angelo Calvão. Através de dados obtidos na internet, no sítio do Tribunal Superior Eleitoral, fizemos uma análise estatística do comportamento dos votos em eleições para deputados e senadores, e em alguns casos para vereadores, desde o período da ditadura até os dias atuais (1970-2014). A análise mostrou que a forma como os votos são distribuídos entre os candidatos reflete a evolução das interações sociais entre os brasileiros. Estas distribuições estatísticas são universais, ou seja, a função que as descreve não muda com o tempo, mas os parâmetros associados mudam. Apesar de ser um sistema altamente complicado, onde cada pessoa numa dada população (cidade, estado, etc) tem suas próprias crenças, convicções, etc, conseguimos modelá-lo de um forma relativamente simples. Para isso, propusemos um modelo matemático baseado em equações diferenciais não-lineares com parâmetros estocásticos, que reproduz bem os resultados observados nos dados coletados tanto qualitativa quanto quantitativamente. Em particular, com esse modelo pudemos associar o principal parâmetro da função que descreve as distribuições de votos com as interações eleitores-eleitores e candidatos-eleitores. Estas interações geram uma espécie de feedback para os candidatos, o que pode aumentar ou diminuir o seu número de votos. O artigo foi publicado na PLoS ONE, e pode ser encontrado neste link.

Um trabalho recente, em colaboração com Celia Anteneodo, discute como as convicções de indivíduos que debatem um determinado tema (como o exemplo sim/não dado acima) afetam o resultado final do tal debate. O modelo mostrou um comportamento bem realista: a presença de indivíduos voláteis, que mudam muito de opinião espontaneamente, assim como a de indivíduos que são facilmente convencidos a mudar de idéia, torna difícil a obtenção de uma decisão final em um debate como o exemplificado. Além disso, mesmo sendo um sistema fora do equilíbrio, mostramos que ele está na mesma classe de universalidade do modelo de Ising, que por sua vez é um modelo de equilíbrio. O artigo foi publicado na Physical Review E, e pode ser encontrado neste link.

Um trabalho recente sobre espalhamento de epidemias, em colaboração com Marcelo A. Pires, levou em conta uma sociedade submetida a uma campanha de vacinação. Além disso, levamos em conta que podem existir nessa população 2 grupos distintos de pensamentos diferentes: indivíduos a favor e contra essa campanha de vacinação. Por simplicidade, consideramos que esses indivíduos se influenciam e podem mudar de opinião a partir da regra da maioria. Juntamente com essa dinâmica de opiniões, uma doença se espalha na população, e essa dinâmica foi baseada no modelo SIS. Consideramos ainda que a vacina pode dar imunidade permanente ou temporária aos indivíduos. Através de cálculos analíticos e numéricos mostramos que as interações sociais entre indivíduos podem afetar drasticamente a propagação da doença, e que o engajamento dos indivíduos favoráveis à vacinação pode ser crucial para freiar o espalhamento dessa doença. O artigo foi publicado na Physica A, e pode ser encontrado neste link.

Um outro trabalho nessa linha, em colaboração com Marcio Argollo de Menezes discute um modelo SIS de epidemias onde a taxa de infecção diminui com o tempo. Apesar de ser um modelo SIS, esta mencionada dependência temporal alterou a dimensão crítica superior do modelo para d=6, que é a dimensão crítica do modelo SIR usual, onde há a presença de uma classe R (Recuperados). Isto permite mapear o nosso modelo no problema de percolação por ligações, ao invés do percolação direcionada como é usual. O artigo foi publicado no Journal of Statistical Mechanics, e pode ser encontrado neste link.

Outro trabalho nesta linha, em colaboração com Silvio Queirós, analisou a eficácia de políticas de auto-isolamento de indivíduos no controle do espalhamento de epidemias. Verificamos que a tendência das pessoas não obedecerem recomendações médicas de isolamento faz com que doenças transmitidas por contato sejam difíceis de controlar. Isto pode ajudar a explicar por exemplo como a gripe H1N1 se espalhou rapidamente pelo mundo no surto de 2009/2010. O artigo foi publicado no Journal of Statistical Mechanics, e pode ser encontrado neste link.

Formação Acadêmica

Linhas de Pesquisa

Nesta área tenho interesse por dinâmica de formação de opiniões, dinâmica de evolução de linguagens, espalhamento de rumores em redes sociais e dinâmica dos contribuintes, entre outros problemas de origem socio-econômica. Os modelos em geral são estocásticos, ou seja, envolvem aleatoriedades que afetam e controlam a dinâmica dos sistemas em estudo. Usualmente tratamos estes sistemas através da simulação dos chamados modelos baseados em agentes, e também através de aproximações analíticas como a teoria do campo médio.

Os modelos baseados em agentes simulam sistemas populacionais, representando cada indivíduo da população por um agente. Cada agente possui características próprias que são armazenadas na memória do computador, e interage com o restante (ou parte) da população seguindo determinadas regras pré-estabelecidas. Sistemas com algum ingrediente estocástico, para os quais contingências ocorridas no decorrer de sua evolução dinâmica são fundamentais, são tratados através da geração de números pseudoaleatórios. O objetivo principal deste tipo de modelagem é capturar interações locais e flutuações que normalmente são perdidas quando tratamos os sistemas por meio de teorias do tipo campo médio.

As redes de interação social são fundamentais na dinâmica de influências entre os indivíduos:

social-media3.jpg

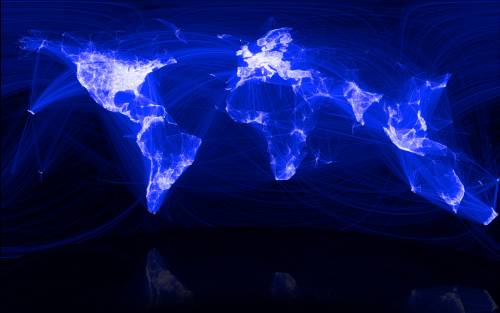
Estas redes podem ser bastante complicadas. As redes de contatos sociais modernas (Facebook, Twitter, MySpace, etc), por exemplo, possuem estruturas altamente complexas e conectam pessoas ao redor de todo o mundo:

facebook_world.jpg

Estas redes afetam a difusão de rumores, opiniões, crenças e outros, entre os indivíduos, e podem ser representadas computacionalmente e matematicamente através de Redes Complexas. Nestas redes cada ponto representa um indivíduo, e dois pontos são ligados se os dois indivíduos se conhecem. A estrutura geral de uma rede complexa é exibida abaixo:

Um exemplo de uma estrutura de contatos do Facebook de 1 indivíduo é exibida abaixo, e é de fato semelhante à representação teórica de uma rede complexa:

facebook_network.jpg

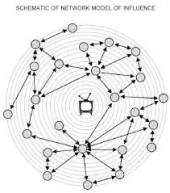
As opiniões das pessoas também podem ser afetadas pela mídia (TV, rádio, internet, etc). É importante considerar nos modelos também a presença de indivíduos formadores de opinião (Opinion Leadears, em inglês):

opinion_network.jpg

Tenho interesse recente por Dinâmica do Sistema Fiscal. Podemos utilizar modelos baseados em agentes para simular o comportamento de decisões dos contribuintes. O objetivo é entender o surgimento de sonegadores de impostos numa sociedade formada por indivíduos inicialmente honestos, e analisar como as punições do estado através de fiscalizações impactam nessas decisões de indivíduos ou grupos. Também podemos analisar o problema de uma forma mais quantitativa, introduzindo cobranças de impostos em transações financeiras dos agentes, através da presença do governo como cobrador. Este tipo de análise pode ser utilizada também para o estudo da dinâmica de sonegação fiscal.

Todos os esses modelos podem ser importantes para entender e explicar o comportamento de pessoas em situações gerais, como eleições, debates públicos, reações ao sistema fiscal, nomeação de objetos, e muitas outras. Além disso, usualmente exibem relações de escala e fenômenos críticos fora do equilíbrio.

Nesta área estudamos dinâmica de populações, modelos de espalhamento de epidemias e processos de ramificação, ou seja, dinâmicas evolucionárias biológicas em geral.

O meu maior interesse nessa área é Epidemiologia. Em geral, estudamos doenças que se transmitem através de contato direto:

tosse.jpg

Assim, as redes de interação entre os indivíduos também têm um papel fundamental no espalhamento de doenças. Este tema voltou a ter força depois dos recentes surtos de gripe A (H1N1), que se espalhou facilmente em 2009/2010 e matou muitas pessoas pelo mundo:

h1n1_pandemic1.jpg

No Brasil, e principalmente no Rio de Janeiro, a dengue é a doença que está mais em evidência, com a ocorrência periódica de surtos na cidade. Ela não é uma doença que se espalha por contato, mas também pode ser modelada, através por exemplo de sistemas de equações diferenciais e redes complexas.

Entender como doenças se espalham é muito importante do ponto de vista teórico e também prático. Estratégias de imunização e quarentena podem ser consideradas nos modelos, de forma a testar políticas de controle de epidemias.

Em relação a Biologia, tenho interesse recente em Dinâmicas Populacionais. A evolução de uma população pode ser estudada através de Processos de Ramificação, muito comuns em modelos biologicamente motivados. Além disso, esses processos podem gerar redes complexas interessantes de serem estudadas do ponto de vista de sua topologia (ou estrutura). Podemos estudar nestes modelos a ocorrência de surtos de crescimento populacional ou de extinção, fenômenos que muitas vezes estão relacionados com leis de potência. No caso de haver outros tipos de funções (exponenciais, por exemplo) governando estes fenômenos, podemos identificar a presença de um crossover na dinâmica populacional, o que pode ser relacionado com uma transição de fase, que por sua vez pode ser caracterizada através de métodos numéricos.

Os modelos acima discutidos normalmente exibem fenômenos críticos. Além destes problemas, também estudamos a ocorrência de transições de fase em modelos físicos, como percolação, processos de contato e magnetismo. Estas transições muitas vezes estão ligadas à existência de estados absorventes, dos quais o sistema, após entrar, não sai mais. Em modelos que estudam a evolução de redes complexas, por exemplo, processos de percolação estão ligados à ocorrência de duas estruturas topologicamente bem diferentes: uma rede fragmentada em vários aglomerados (ou clusters) e uma rede com um aglomerado que ocupa quase toda a rede, o chamado aglomerado gigante (ou cluster gigante). Um exemplo ilustrativo dessa transição de fase geométrica é mostrado a seguir:

alpha0.5-n500.jpg alpha0.01-n500.jpg

Esta é uma área mais recente de trabalho. Redes de transporte são sistemas desenvolvidos para o transporte eficiente de matéria. Como exemplo temos carros em estradas, pacotes na Internet, nutrientes em células, grãos em silos, e muitos outros. Um fenômeno comum a todos estes sistemas é o congestionamento do tráfego, causado pelo volume finito de matéria que pode ser transportada na rede e pela capacitade limitada dos canais de transporte. Fazer previsões sobre congestionamento de tráfego nesses sistemas é um problema de grande interesse prático, e tem motivado uma grande quantidade de esforços em pesquisas interdisciplinares.

Uma questão de interesse é otimizar o transporte de matéria em redes. Pensando em uma cidade, por exemplo, otimizar estaria relacionado a minimizar os tempos de deslocamento entre dois pontos quaisquer da cidade. Isto é atualmente um questão de grande relevância, já que as grandes cidades brasileiras como o Rio de Janeiro possuem problemas sérios de congestionamento:

transito_rj.jpg

Além disso, também tenho interesse recente por Mobilidade Humana. Entender como as pessoas se movimentam em cidades é um tema importante de pesquisa, já que pode impactar em melhorias no transporte público, por exemplo. Além disso, o espalhamento de doenças está intimamente ligado à movimentação diária das pessoas, e o estudo de mobilidade pode ajudar também no controle de epidemias. Nesta área tenho colaborado com engenheiros da COPPE da Universidade Federal do Rio de Janeiro e com pesquisadores da Fundação Getúlio Vargas.

Publicações

Trabalhos em Andamento

Livro

livronuno.jpg A minha dissertação de mestrado foi publicada em 2010 em formato de livro pela editora Lambert Academic Publishing da Alemanha, com o título Phase Transitions in Disordered Systems under Random Magnetic Fields. Neste livro, eu discuto os efeitos de desordem local, tanto nos acoplamentos entre os spins, quanto no campo magnético, nos diagramas de fases de modelos de Ising, utilizando a teoria do campo médio. Estes modelos são de grande interesse teórico, já que exibem um comportamento crítico muito rico. Além disso, podem ser realizados experimentalmente em materiais antiferromagnéticos diluídos, tais como Fe_{x}Mg_{1-x}Cl_{2} e Fe_{x}Zn_{1-x}F_{2}, na presença de um campo magnético uniforme.

Colaborações

Seminários

Apresentação de Trabalhos

Revisor de Periódico

Membro de Corpo Editorial

Workshop RioBio

RioBio: ciclo de seminários interdisciplinares em biomatemática, bioinformática, biofísica, …

Para maiores informações, visite a página do evento

Ensino

Música

“A arte é livre e aberta, a imagem do ser criador, samba é verdade do povo, ninguém vai deturpar seu valor” - Candeia

Imagens

camisao.jpg portela.jpg

Contato

Instituto de Física
Universidade Federal Fluminense
Av. Litorânea s/n, CEP 24210-340
Niterói - Rio de Janeiro
E-mail: nuno@if.uff.br, nuno@mail.if.uff.br
Sala: 419, torre nova do IF
Telefone: (21) 2629-5845

Locations of visitors to this page

logouff.jpg logo-pt-br.jpg
cnpq_v9.jpg